Requisite-variety and stormy weather
Just how much of a law is Ashby’s Law of Requisite Variety? Our answers to that question – and likely there’ll be many of them – are fundamental to how we handle key architectural concepts or requirements such as management, control, certainty (or lack of it), complexity, disruption and much, much more.
Okay, first, the nominal law itself, as summarised in Wikipedia:
If a system is to be stable the number of states of its control mechanism must be greater than or equal to the number of states in the system being controlled.
Or, as summarised by Stafford Beer, in relation to variety in viable systems:
[variety is] the total number of possible states of a system, or of an element of a system … the logarithmic measure of variety represents the minimum number of choices (by binary chop) needed to resolve uncertainty.
In short, control is possible in a context only if the controlling mechanism can manage a range of variety at least equal to or greater than the variety inherent in the context itself.
Which, if we think about it for more than a few seconds or so, tells us that absolute control is all but impossible in the real-world, because there are so many real-world items – nuclear fission, to give one well-understood example; or customer-service, to give another less-well-understood example – that present near-infinite variety or uncertainty.
Hence, in short, control is a myth – a futile fantasy of wishful-thinking. Oh well.
But just wait a minute, you might say – how come we seem to have control of most things for much or most of the time? Which is true enough – sort-of. And it’s in that ‘sort-of’ that things get kinda interesting… and where those answers to the ‘law-ness’ of Ashby’s Law get kinda important.
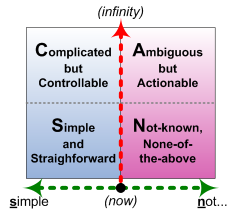
Quick background to all of this is that a couple of days ago I was trying to explain to a colleague how to use the SCAN sense-making/decision-making framework:
In particular, I was exploring with him the conditions and contexts in which we switch from side to side of the Inverse Einstein Test (the central red dividing line in the graphic above) – the point at which doing the same thing leads either to the same results (left side: Simple/order) or to different results (right side: Not-known/unorder).
And the key realisation is that, in the real-world, that boundary-condition will itself keep moving around. Sometimes doing the same thing will give the same results – in other words, what we might typically think of as ‘control’. And sometimes it won’t give the same results – which means we’re not ‘in control’. Despite doing exactly the same things, and following the same nominal ‘laws’. Tricky, that…
So sometimes we’re in control. And sometimes we’re not. Of the same nominal context.
Or, to put it another way round, there’s variety in the variety of the context.
Or, in yet another way to frame it, Ashby’s Law is recursive: if it’s a true law, it has to apply to everything – including itself.
Which suggests in turn that we perhaps need to re-think the variety of a system as being more like the uncertainty of weather, rather than some kind of fixed numeric value:
- Variety is not a state, but dynamic, itself varying over time.
Hence sometimes there are periods of calm, when the variety in the system is low. This is what gives us that so-desirable illusion of ‘control’.
Sometimes there’ll be long periods of calm, when we get lulled into thinking that our ‘world’ – whatever that might be – will stay the same forever.
And then sometimes it’s ‘stormy weather’, when we get a firm reminder that ‘control’ is indeed an illusion….
Sometimes those periods of stormy-weather can go on for a long, long time, in which nothing seems stable or certain – the kind of ‘world’ we’re often dealing with in enterprise-architectures right now, in fact.
So whilst in principle Ashby’s Law would always hold, perhaps it might be useful to think of variety in a way analogous to weather-forecasting:
— Sometimes the variety-weather will be calm: in which case we can trot out all of those tried-and-tested management-methods, and be reasonably certain that they’ll work well. For the while, until the variety-weather changes.
— Then sometimes it turns stormy: in which case we need to acknowledge that those ‘control’-based methods won’t work in that context, and we need to shift over to the different disciplines of design-thinking and the business-anarchist and suchlike. For the while, anyway.
The trick is to watch the variety-weather, so as to know when to change methods. And at the present time there doesn’t seem to be any systematic approach to this: skilled business-folk do it more by ‘feel’ than by anything else, it seems.
So perhaps it’s time for a new science (or craft, or technology, or some such) of ‘varietology’, or something like that – an equivalent of meteorology, to monitor the variety of the variety-weather in our business context?
And if so, what would it look like? What are the key factors behind the variety of the variety? What forms do they take? – how do we experience this variety-weather? And how could we make sense of all of those factors – or of the sense-making itself?
Comments / suggestions, anyone?
Councillor Harmann: Down here, sometimes I think about all those people still plugged into the Matrix and when I look at these machines I… I can’t help thinking that in a way… we are plugged into them.
Neo: But we control these machines; they don’t control us.
Councillor Harmann: Of course not. How could they? The idea is pure nonsense. But… it does make one wonder… just… what is control?
Neo: If we wanted, we could shut these machines down.
Councillor Harmann: [Of] course. That’s it. You hit it. That’s control, isn’t it? If we wanted we could smash them to bits. Although, if we did, we’d have to consider what would happen to our lights, our heat, our air…
Neo: So we need machines and they need us, is that your point, Councilor?
Councillor Harmann: No. No point. Old men like me don’t bother with making points. There’s no point.
Neo: Is that why there are no young men on the council?
Councillor Harmann: Good point.
🙂
Neo: Why am I here?
The Architect: Your life is the sum of a remainder of an unbalanced equation inherent to the programming of the matrix. You are the eventuality of an anomaly, which despite my sincerest efforts I have been unable to eliminate from what is otherwise a harmony of mathematical precision. While it remains a burden assiduously avoided, it is not unexpected, and thus not beyond a measure of control. Which has led you, inexorably, here.
🙂
[A couple of semi-serious jokes about control – or the myth of it.]
The paradigm behind Ashby’s Law is that of a simple system with mechanistic, programmatic adaptation. It is essentially a hard systems approach built on the assumption of fully deterministic systems driven by strict causality.
Ashby’s Law can be escaped by systems that are capable of recognising and understanding new situations – stormy weather – and adpating appropriately. Systems that are truly intelligent – systems that can model their own context and to an extent predict its evolution (and their own) – and expect it. Systems that can change their thinking, that can identify the assumptions on which it is based and change them – systems that can do double-loop and triple-loop learning (a la Argyris and Schon). Systems like an Enterprise Architecture informed proactive management. Because stormy weather is expected while it may be assiduously avoided it is not beyond some measure of control. 🙂
Ashby’s Law applies to non-learning, non-knowledge-creating systems. Organisations can choose to be like that… …or not.
The science you refer to has been around for a number of years – although is not often organised in the way you [one] might expect. It comprises a modern synthesis of ‘systems thinking’ (in the general sense encompassing General Systems Theory, Soft Systems, Sociotechnical Systems, Systems of Systems etc. and including the spectrum from low-number, deterministic control to large-number statistical control), complexity theory – including chaotic systems and emergence – and bits of Schumpeterian economics and financial mathematics.
What is missing is the application of such scientific methods to organised and semi-organised systems of sociotechnical systems – like the banking industry, the financial markets, monetary unions etc. Methods that would describe and predict the behaviour of such systems in probabilitic terms.
[BTW: Did you note the analogy to entropy – logarithm of possible states? Knowledge generating/wielding systems can also escape the Second Law of Thermodynamics. ]
Happy to discuss.
Regards,
Ian.
Tom I think we talked a little about Ashby last time you visited us at DSTL. Good to see the treatment you have given it above and some interesting comments from Ian. If either of you are interested I have read what I would say is interesting, if a little academic, stuff from a professor Jc spender recently. Happy to forward. Let me know if you want a link. On my phone at the mo however and running out of batter
Good points about Ashby’s law, particularly how it relates to SCAN.
Part of my take on Ashby’s law (based on where I first learned about it) is that it’s not just the number of states, but the number of dimensions and the degrees of freedom that have to be matched. Consider a plane landing on an aircraft carrier at sea. In perfect weather, you could use a traditional scientific management approach to control and successfully land the plane by using prescribed settings of throttle and “stick.” But in a bad storm, if the wind blows you 20 feet to the left, up 5 feet, back 13 feet, and drops your airspeed by 30 knots, you have to counteract in all four “dimensions” of variability, or you’ll miss the landing deck.
Another aspect of the number of states, is that the Viable System Model talks about attenuation and amplification around the control function. In some cases this can allow a control with a smaller range cope with a larger range in the environment. However it rarely works for the control to work in fewer dimensions of variability.
This also ties in with Theory of Constraints. You can think of each constraint as another dimension of variability. You get “unpredictable” results when you loosen a constraint that is a bottleneck (in yourself or the environment), only to run into another constraint that becomes the new bottleneck.
Nice blog site. Still a breath of fresh air today, given the continuing state of “enterprise architecture” I see at most places and sites.