Comparing SCAN and Cynefin
Sensemaking in business? What is this [choose-your-expletive] ‘SCAN‘? Why complicate things with yet another sensemaking-framework? Isn’t SCAN just a rebadged rip-off of Cynefin? And why not just use Cynefin like everyone else does, anyway?
I’ll be providing some detailed worked-examples of SCAN in the next few posts or so, but I’d better get these questions out of the way first, because otherwise someone or other will jump at me about it if I don’t. The quick answer is, yes, there are solid reasons for all of this, and no, this isn’t ‘having a go’ at Cynefin or anything else. Okay?
To answer each of those above questions in turn:
- making sense – and making sense fast – of things that don’t yet make sense, is an essential business requirement, in enterprise-architecture and in just about every other business-discipline
- what we often need for business-sensemaking is something simple, fast, and easily memorable, yet also has all the sensemaking depth behind it – and SCAN supports that need
- the aim is to simplify, not complicate – the main reason for SCAN is to uncomplicate something that’s become almost hopelessly complicated and problematic
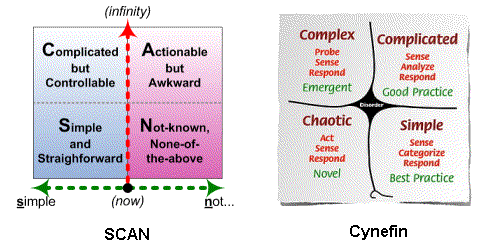
- the two frameworks may look similar on the surface, and I’ve intentionally designed SCAN so that they can be used in parallel, but they actually have significantly different roots, roles and methods
- in practice, in most of the business-domains I work in, usage of Cynefin seems a bit like TOGAF for enterprise-architecture – just about everyone says they use it, but almost no-one actually seems to use it as per the published specification
That last point has lead to lots and lots and lots of fights over the past few years: too many fights, between too many people, in which I’ve too often found myself in the painful position of pig-in-the-middle… So in the hope that it’ll defuse some of the drivers for at least some of those fights, what I’m aiming to do here is:
- separate out two fundamentally different types of sensemaking – ‘considered’, versus ‘business-speed’
- explicitly acknowledge that Cynefin fits well with the needs of ‘considered’ sensemaking
- describe how and why Cynefin has proven problematic in ‘business-speed’ sensemaking
- how SCAN sets out to resolve each of those issues, specifically for ‘business-speed’ sensemaking
There’s some overlap between SCAN and Cynefin, obviously, because both are tools for general-purpose sensemaking; but the key point is that they serve and emphasise different business needs.
Business roles
Making sense, to support good decision-making, is an obvious business need.
In practice, there are two fundamentally-different kinds of business sensemaking:
- ‘considered’ – analysis and experimentation, classically done by consultants, professionals, senior management and strategy staff
- ‘business-speed’ – categories, checklists and personal judgement, classically done by line-managers, supervisors and front-line staff
The crucial distinction is available time. If we had the time at the front-line to make a proper ‘considered’ assessment and decision, we’d do so: but we rarely have that luxury. So at ‘business-speed’ we have to make do with a different kind of sensemaking: it’s not as pretty, not as precise, not as ‘scientific’, but it’s pragmatic and practical. Simply what works, at the time, in the time available.
In other words, both kinds of sensemaking are ‘true’, for a given value of ‘true’. The practical question is about which kind is more appropriate – more useful – for a given business need.
Cynefin explicitly positions itself for ‘considered’ sensemaking. To use the Cynefin terms, it emphasises the Complicated and, especially, the Complex domain. I believe it’s fair to say that it aims to elicit insight and understanding by focussing on nuance and subtlety, on emergence in complex adaptive systems, and so on. We do get the most ‘scientific’ results this way: but it takes time.
SCAN explicitly positions itself for ‘business-speed’ sensemaking. To use the Cynefin terms, it emphasises the interplay between the Simple and Chaotic domains. It uses classically simple-yet-powerful techniques such as recursive checklists, to access the full depth of sensemaking whilst still maintaining full business-speed.
In short, the frameworks’ roles and emphases are not the same: as above, they’re both about sensemaking, but they service somewhat different business needs.
Framework roots
Cynefin’s roots go back to at least 1999, and are primarily in the sciences. As its Wikipedia page puts it, “the Cynefin framework draws on research into complex adaptive systems theory, cognitive science, anthropology and narrative patterns, as well as evolutionary psychology”.
SCAN’s roots go back to at least 1986 (the ‘swamp analogy‘ for sensemaking), and are primarily in pragmatics. There’s a lot of science and more behind it – for example, on Jungian psychology and the tetradian, cognitive psychology, textual deconstruction, real-time learning and real-time decision-making – but the focus is always on real-world practice.
In other words, one has a science focus, the other a technology focus. It doesn’t make much sense to try to assess either one solely in the other’s terms.
Practical problems with Cynefin
This section describes some practical problems that I and others have often come across whilst trying to use Cynefin with everyday business-folk in enterprise-architecture and the like – in other words, primarily in contexts that demand ‘business-speed’ sensemaking. I’ll also describe how SCAN addresses and, I hope, mostly resolves each of those problems.
I know it sounds petty, but often the first hurdle is just the name ‘Cynefin’. Even the pronunciation is problematic: I’ve come across several people who’ve talked excitedly about ‘sign-fin’ – which is how standard-English would (attempt to) pronounce ‘cynefin’ – and get very confused when someone else uses the proper Welsh-style pronunciation ‘kuhnevin’.
[It’s not that the Welsh pronunciation is ‘wrong’, because obviously it isn’t. It’s just that it confuses people, and gives an unfortunate impression of an ‘in-group’ who know how to pronounce it properly, versus an ‘everyone-else’ who don’t.]
By contrast, SCAN is pronounced exactly as per the standard-English spelling.
We’ve had similar problems around the meaning of ‘Cynefin’. The Wikipedia page explains it as follows:
Cynefin is a Welsh word, which is commonly translated into English as ‘habitat’ or ‘place’, although this fails to convey its full meaning. A more complete translation of the word would be that it conveys the sense that we all have multiple pasts of which we can only be partly aware: cultural, religious, geographic, tribal etc.
In practice, with front-line managers, I’ve possibly lost them at the first word, probably lost them at ‘Welsh’, and definitely lost them by the time we bring ‘habitat’ or ‘place’ into the picture – let alone ‘multiple pasts’ or anything else. I then have to do quite a long explanation as to how and why, yes, this is about business-sensemaking, and it’s useful and important. That’s if they allow me any time to do it, which often they don’t… which doesn’t help.
[Again, this is purely pragmatics: the richness and depth of the word ‘cynefin’ is indeed valuable, yet the lack of self-description in the name makes it that much harder to get started.]
By contrast, SCAN says straight away what it is and does: we do a scan through the context to make sense of what’s going on.
Cynefin also depends on special meanings of common terms. The worst problems have been around ‘complex‘: Cynefin uses this in the specific sense as in complexity-science, but that’s landed us with huge arguments with IT-folks and others who’ve always used ‘complex’ to mean ‘very complicated’. We’ve had similar arguments around ‘complicated‘ itself; and likewise ‘chaos‘, which Cynefin uses in an uncommon way, quite different from the colloquial usage. Even ‘simple‘ has turned to be not as simple as we’d thought.
[Once again, this is purely about pragmatics: those special-meanings in Cynefin do enable much more precision, but at a significant cost in understandability and versatility, especially at ‘business-speed’.]
By contrast, SCAN provides suggested, colloquial terms for what are essentially similar sensemaking-domains to those in Cynefin, but beyond that it leaves terminology intentionally open. Surfacing personal interpretations of terms thus itself becomes part of the sensemaking process.
In my experience, perhaps the most serious problem has been that Cynefin presents way too much scope for methodological confusion – and especially so when people try to use it for sensemaking at ‘business-speed’, where everything will be pared down to the bone, whether we like it or not. The most obvious of these confusions is that it looks like a straightforward two-axis matrix – which it isn’t. Visually, it’s presented as a categorisation-framework – which it isn’t. (Or is. Or isn’t.) There are those four straightforward domain-categories that everyone sees – the SCCC-categorisation of Simple, Complicated, Complex and Chaotic – but then there’s the fifth-domain of Disorder – which is both a domain in its own right and the backplane for everything else – and the ‘squiggle’ – which frankly takes too much effort to explain.
Then there are all the Cynefin methods behind it, which in principle are grounded in complexity-science and so on, but often don’t match up with how most people understand ‘complexity’ in just about any discipline other than complexity-science. In sensemaking at business-speed, we simply don’t have time to do that kind of translation between disciplines – hence no surprise that key nuances get lost in the non-translation. And the general opacity and special-meaning-after-special-meaning of the methods mean that there are – as I and far too many others have discovered the hard way – all too many options for ‘illegitimate’ usage of Cynefin, and not many ‘politically-correct’ usages that actually do make practical sense in our work-domains. So in practice we end up saying, yes, it’s a sort-of four-category framework that isn’t, sort-of, that’s why it has those pretty curved boundaries, sort-of – and then just kind of hope for the best, hiding behind cautious phrases such as ‘inspired by Cynefin‘ and suchlike. Which is not a good way to use anything.
Sure, Cynefin’s terminology is wonderfully precise, and likewise its methods: in skilled hands, and given enough time, it really can work wonders. But in practice, all too often, it’s been a bit like letting business-folk loose on a typical EA toolset: it’s so dependent on everything being done exactly right, that it doesn’t take long for the whole thing to turn into an impenetrable tangle of misunderstandings and confusion – the exact opposite of what we’re aiming for in business-sensemaking. And for ‘business-speed’ sensemaking, we simply don’t have time to sort out that kind of mess.
[A reminder again that I’m not saying Cynefin is ‘wrong’ – because clearly it isn’t. All I’m saying is that these are the kinds of methodological problems that I’ve seen arising time after time, in real-world practice, in enterprise-architecture and the like.]
By contrast, SCAN is bald and straightforward: it makes no pretence of being more than a simple cluster of four categories, arising from a plain ordinary two-axis matrix – and if we want to, it can be used, and useful, just like that, with nothing else. (In fact it can even be used as a single-axis ‘matrix’ – the tension between Simple and Not-simple, known and not-known.) It can, however, also go a lot deeper than that – yet all still with the same set of categories, all of the way.
A bit more detail on SCAN
The real power of SCAN comes not from the frame itself, but from what happens when we use that frame in conjunction with an equally straightforward set of systems-thinking principles. We can use those principles to any extent and any depth that we need – including none at all.
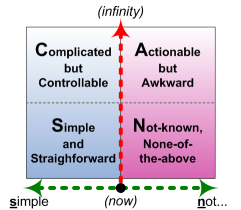
To use that usefully-precise Cynefin terminology, we could split those principles as follows:
- Simple: repetitive rotation between multiple views or perspectives or focus-themes – such as in a checklist or, here, a simple four-category frame
- Complicated: reciprocation – balance across a system – and resonance – the ‘snowball effect’ (positive-resonance) and damping (negative-resonance)
- Complex: recursion – self-similarity at different levels – and reflexion – patterns, particularly ‘the whole contained within the part’
- Chaotic: cognitive-dissonance – deliberate-mismatch to trigger ideas – and serendipity – allowing ideas to arise in unexpected ways
In terminology that might be more familiar for enterprise-architecture folk, this is about iteration and allowing emergence of new ideas and requirements, much as in any of the Agile development methods. It’s done at real-world speed, not ‘sit-and-think-about-it’ analysis-paralysis; there’s an explicit architecture to it, but it’s not the old Waterfall-architecture of ‘big-requirements-up-front’. It’s kept as simple as possible, but it’s not simplistic: there’s real depth behind it, whenever we need.
What we’re after – one of our key success-criteria – is when someone says, “Oh, I hadn’t thought of it that way…”, and then develops the whole discussion in a new and different direction. In other words, useful insights, arriving ‘from nowhere’, at business-speed.
In essence, SCAN is a ‘stealth’ form of context-space mapping. For simplicity, it’s constrained to a single type of base-map, but we can still apply any other overlay – including the Cynefin frame – to use as a cross-map in conjunction with any or all of those systems-thinking principles above. So it’s simple enough, and familiar enough, not to scare people off: yet we can go down into whatever depth we desire – or dare – in whatever little time as there may be available to do it.
Different trade-offs, different roles
To me, as a practitioner, I’d guess that the key difference between Cynefin and SCAN is that they make different trade-offs between precision versus flexibility, sophistication versus simplicity, and several other suchlike themes. Perhaps the best way to illustrate this difference would be the comment of an old friend of mine, who said that his greatest challenge as a mathematician working in aircraft-design was to make his mathematics sufficiently imprecise to be useful.
Another anecdote comes to mind here, a conversation some years ago in Lisbon. One of the people there was passionately holding forth about the inadequacies of English as a language: “We should all be speaking French!”, he exclaimed. “French is the language of diplomats! It is exact; it is precise.”
“The advantage of French is that it’s precise”, was the quiet reply. “The advantage of English is that it isn’t.”
Cynefin’s advantage is that it’s precise, a science-based ‘language’ appropriate for the needs of complexity-consultants engaged in ‘considered’ sensemaking.
SCAN’s advantage is that, by intent and design, it isn’t precise – which makes it a better fit for the more pragmatic needs of ‘business-speed’ sensemaking.
Different trade-offs, different roles.
Different choices.
But probably important that we don’t mix them up?
Over to you for comments and suchlike, anyway.
I like it but with one reservation: I don’t like the word “awkward.” Negative connotation, when to my mind the situation you mean to describe there CAN be full of wonder. Is there a more positive word (that starts with “a”) to describe what you mean? Alive? Aggregate? Abstruse? Amazing? Ample? Atypical? Awe-ful? Astounding? Awesome?
It’s too bad that “awful” stopped meaning anything positive, because it used to be a great word for complex emergence. You could go with awful/awe-ful. It’s a thought but then you are back in having to explain what a word means which is what you don’t want, and a good point too.
My confluence framework, I think, stands far away from “business-speed” and is for we snails of thought inching our way across the damp soils of reality.
Also, have you seen Jurgen Appelo’s model?
http://www.noop.nl/2010/09/simplicity-a-new-model.html
it has a useful outlook, I think, and similar goals. I don’t quite get it — too tainted by fixed ideas of what “complex” and “complicated” mean, and I get stuck on things like “what does it mean to understand something?” — but it seems useful nonetheless.
Hooray for many ideas and frameworks! It means we are all ALIVE, and isn’t that great?
Cynthia! How Awesome to hear from you! Amazing! Anaglyptic! Analogical! And other such A-words!
To be honest, I started with Agile for the ‘A’, but, yeah, it wasn’t right. ‘Awkward’ was about the closest I got to in the sense that I wanted that feeling of uncertainty, of ‘Inverse Einstein’ (see the previous post) where we do know what’s happening, all that we know is that we’re not in control any more but it’s still sort-of-working in its own way. “Kinda awkward… how’re we gonna explain this one?” – that kind of feeling.
But yeah, I’d much prefer a better ‘A’-word. It’s just I haven’t found one yet…
Confluence framework – actually, I disagree: don’t underestimate it. Snails of thought, yes, but sometimes those snails have wings, and more? 🙂 Particularly with those roots in the Medicine Wheel, it should be able to reach right down into real-time speed far better than my ‘patch-job’ can, and likewise possibly quite a lot deeper than Cynefin at the other end of the scale. (The original Welsh sense of time and place would, I imagine, be every bit as deep as that of the Medicine Wheel, but our frameworks kida get in the way, don’t they? 😐 ) I’m well aware that SCAN is a ‘patch-job’ – on the surface, anyway – because that’s all that most people seem to be able to take: the ‘trick’, so to speak, was putting something together that was really simple on the surface but still had all of the hooks to go deeper as required. I think it will hold together well enough for the rough-and-tumble at the near-real-time end of the scale, but time will tell, obviously.
I haven’t seen Jurgen’ model, but from his well-received recent slidedeck I know he’s a fan of Cynefin, and hence its concept of complexity. That was actually the source for SCAN: I had three major players from different parts of the enterprise-architecture space – IT, people-consultancy and security – all earbashing me about the constraints of the Cynefin ‘the complex’, and how it didn’t fit with their world at all. That’s when I realised that the best definition would be no definition at all: we could imply enough to act as a hook in each domain, but then using the sensemaking process itself to elicit and resolve all of the different understandings of terms and the like. In effect, recursion on complexity itself – something that we’re apparently not supposed to do with Cynefin, but I’ve always found all but essential in practice.
ALIVE! – yes indeed! 🙂 Let’s keep in touch on this, anyway. And thanks, of course!
Additional, post-bath thought. (Cut short my bath, damn you! Penalty: chocolate. Does this thing record what time of day people take baths?)
If there is to be a league of people who build and explain frameworks, it should have some rules. I nominate these:
1) You may say your framework is “my” or “our” or “a” framework. You may NOT say your framework is “the” or the “correct” or “only” framework.
2) You are obligated, whenever your framework is presented in any form, to either (a) list other similar frameworks or (b) mention that there ARE other similar frameworks about which information can be sought by those interested.
3) This list of similar frameworks you must build, maintain and improve assiduously. You must keep in the list every framework you honestly know to cover similar topics, even if you don’t like the behaviour of the person/people who built them. You may not exclude frameworks and models created by people you do not consider qualified to create a framework or model due to insufficient credentials, wealth, power, gender, origin, religion, whatever. The quality of each framework in use, not as YOU find it but as HUMANITY finds it, is what matters. In other words, if you know of a framework, find it unbearably stupid, but happen to know that dozens or thousands of other people derive much benefit from it (so they say and in public) you may not exclude it from your list.
4) When you explain your framework, if anyone says “I have no idea what you are talking about” you may attempt to explain your framework for as long as your patience and theirs holds out. However, beyond that point, if they STILL do not understand, you are obligated to point them to your list of other similar frameworks to see if any of those make more sense to them. You may not say that if people do not understand or cannot fruitfully use YOUR framework they do not (or cannot) understand the issues it addresses.
Having thought about these rules I noticed that I had broken one. Even though I put that link to Jurgen Appelo’s model in my comment here I didn’t have it in the list on my page for the confluence framework. This was not because his model is flawed but because he was a bit snippy in telling me about it, and that sort of thing always freaks me out. Rule broken, list augmented, rule mended.
Over to you?
Cynthia – My apologies re bath (‘Eureka!’ moments have their own sense of time, I fear… 😐 🙂 ). If you wish to return the unfavour, my shower-time (not bath, can’t remember when I last had a bath… all I remember was that it took several sessions with the osteopath to straighten my neck out again afterwards…) is somewhat just after your midnight. (Yep, I get up early.)
Courtesy of a different blog-post I’ve just been reading, I have just found the obvious ‘A’-word: Ambiguity. Of course. 🙂
Re ‘the framework-headed league’ – nice one indeed. Reminds me of the town of Hay-on-Wye, on the English/Welsh border, whose main business is second-hand bookshops (down, girl, down! 🙂 and anyway there is a baggage-limit on the plane home… 🙁 ) – see bookshops. It all works because they cross-sell like crazy – everyone markets everyone else. That way you get breadth (across the whole town) and depth (in the specialism of each individual bookshop). Yet it would fall apart if one firm tried to set itself up as ‘the only bookshop’. (Apparently Waterstones or some such tried it at one point, and got quite firmly kicked out of town.) Should be the same with frameworks, yes?
And yes, I’ve broken those rules rather too often – in one direction, certainly… 😐 I do believe we should still evaluate and review, in the same way that a bad bookshop could wreck the Hay-on-Wye market – but it should be on genuine grounds of quality, in its own terms, not simply because we happen to dislike it.
Very good point, anyway.
I love ambiguous. Only I would say it as “ambiguous but actionable” matching your other three as what-it-is then what-you-can-do. And it is perfect that the N-spot does away with what-you-can-do because it’s not that simple there. I also like how you have “but” on the top and “and” on the bottom, which is meaningful.
I used to think for a long time: why should I write anything since all the great books have already been written? And then I came to understand that for every book, no matter how idiosyncratic and historical and unique, there is SOMEbody for whom it is the perfect book at the moment when they encounter it. Because people are diverse books must be diverse. The same thing holds for frameworks and models. If one model worked for everyone, we would all be the same, and CLEARLY we are not. So I can only be overjoyed when I see a new model taking shape, even if it is the child of a model decades old.
Actually I don’t UNDERestimate the CSF when I say it is for snails, I OVERestimate it. To my mind the snails always have the last laugh, and this is far more true for those who first built their frameworks thousands of years ago than for anything I could come up with. The day when I found out about the medicine wheel, all ideas I had of “prominence” or “credentials” or “dominance” or “importance” flew away. Mice at the foot of a mountain.
One of my favorite discoveries in children’s books has been the book “Paddle to the Sea.” It is about a Native American boy who whittles a little wooden boat, with rider, and marks on it the words “I am Paddle to the Sea. Please put me back in the water.” The little boat makes its way through the Great Lakes system all the way to the Atlantic ocean. At the very end of the book, a French trapper and American sportsman loudly exclaim about a newspaper article telling how the little boat made it all the way to France. Then the book says:
—————
The third man on the wharf was a young Indian, tall and strong. In his mocassins he moved so silently across the dock that the others did not hear him. He took one long look over the Frenchman’s shoulder at the paper.
“You put him back in the river and sent him on? Good. I made that one,” he said softly, and turned away.
The young man had stepped into his canoe before the Frenchman spoke again. “What that Injun say jus’ now?” he asked, laying the paper aside.
“Didn’t hear him,” replied the sportsman. Both of them glanced toward the river, but the canoe was already moving away under steady strokes of the paddle. So the two men returned to their important thoughts.
In the canoe, the Indian smiled. Once he paused in a stroke, and rested his blade. For that instant he looked like his own Paddle. There was a song in his heart. It crept to his lips, but only the water and the wind could hear.
—————
So: we should ALL build our frameworks and set them down in rivers of thought. Then, if and when we find them again in some new ocean, we can paddle away with a song creeping to our lips for the water and the wind to hear.
I was just wondering how this might help with decision making (after sense-making). For example when doing EA work and confronted with a new situation and the nature of it. Is it something simple, that can just go ahead, is it complex and I need a plan, is it actionable but I need some form of governance, should I refactor the problem in an attempt to make it more simple? Some more grist to the mill? I like it, keep going, management is both an art and a science, so if the framework helps shape thinking then it does not need to be completely exact. A new creative thinking tool?
Stephen: re “how this might help with decision-making (after sense-making)” – I think it’s often a mistake to separate them. For example, consider John Boyd’s OODA-loop, or Agile-development processes, or even the venerable PDCA quality-improvement loop: they’re all continuous-cycle in which sense-making, decision and action are intertwined. (This is especially clear in OODA: Observe [what’s going on], Orient [sensemaking], Decide [decision-making], Act [action] – all at very high speed.) So in that sense, not new as such.
But yes, I guess there is something somewhat new here, in that we’re applying the same categorisation to decision-making as to sense-making, so in a way the sensemaking – and, as in your example, a recursion on the sensemaking – itself acts as a pre-filter on the decision-making. I’d kind of implied that in various posts before, but you’re right, it needs to be made much explicit. Will include that in some of the upcoming examples – many thanks for that.
Tom, Just as an after-thought, if your idea goes far enough, you could combine it with some of your gaming ideas and implement it as a sensemaking / decision making gaming iphone app?
Are there any other unexplored phone app opportunities for business? In two years time, the arm smartphone processor will be 10 times more powerful than what it is today, new opportunities abound?
Stephen: to be blunt, almost all of these ideas I’ve been working on and describing over the past year or so would work really well as smartphone/tablet apps.
The graphics-oriented tools such as Enterprise Canvas would be somewhat of a swine to get going – mainly because of the need to provide continuous feedback whilst drawing a line, which I don’t know how to do – but the rest, frankly, should be almost a doddle to get going. Looking at Dave Gray’s really nice Gamestorming app that was released today (I think?), it should be quite easy to set up a ‘This’ game as an extendable card-based app – the main difference would be some mechanism to store the results, and probably upload/share them with a remote EA-tool repository.
As for SCAN, the frame itself is so simple – it’s just one card – that there would be little or no value in an app to do that alone. The value-add would be in what happens with the SCAN frame. For example, tagged voice-recording / text-recording, somewhat like AudioNote on the iPhone/iPad. Or use ‘post-its’ on each of the quadrants – a bit like BMTBox, the iPad app for Business Model Generation – but build a stack of SCAN cards, much as per the Gamestorming app but with multiple copies of the same card with different post-its to show different parts of the sensemaking / decisionmaking process.
My real difficulty here is that I don’t know how to do iPad/iPhone programming, and after a couple of week of struggling with the ghastliness of Apple’s ObjectiveC, I’m not exactly keen to fight with it any further! So if you happen to know any good app-programmers who are looking for what could be a highly-commercial app-idea, perhaps let them know? 🙂
@Tom G
People issues and situations are often very ‘Complex’, business problems tend to ‘ Complicated’, technology often borders on ‘simple / Complicated’. My response to ‘Chaotic’ things tends to be an attempt to move it into ‘Complex, Complicated or Simple’, I would very rarely just respond to something Chaotic without trying to understand it first e.g. just react without thinking (or at least try not to). So the Cynefin framework sort of works for me in a very heuristic sort of way, except I find the action of ‘Respond’ a bit too abstract to apply in a particular e.g. work context. So within a particular domain e.g. EA, the logic, thought patterns and actions might be more specific, currently very tacit, but, perhaps via a decision framework could be made more explicit? In Summary, the Cynefin model clarifies how I think, I guess what remains is how do I actually respond, and that would be context specific? Perhaps it is just a matter of levels of abstraction and addition of context between the methods? Obviously, the easier it is to grasp a method the more likely it will acquire adoption? My brain is starting to hurt now, so I will shut up 🙂
@Stephen – Yes, that’s how I used to use Cynefin in EA work: and I got shot at for doing so, in no uncertain terms, because it’s not ‘correct’-Cynefin. Hence, yes, I ought to gently warn you off that particular interpretation, because it can be, uh, problematic…
One of the important differences between SCAN and SCCC-categorisation – i.e. what most people seem to think of ‘as’ Cynefin – is around what you’ve described above as the Chaotic. As you say, the typical view of the Cynefin ‘respond’ is “act / sense / respond”, to pull it into one of the other domains. (However, I’ve been told this specific interpretation of Cynefin and the Chaotic is wrong, so I won’t interpret any further – other than to note that this is a typical example of the ‘methodological confusion’ I described in the post above.)
One of key things I found in my struggles in this area is that highly-skilled people (particularly troubleshooters, improvisers, stock-traders and so on) actually spend much if not most of their time in what the SCCC-categorisation classes as the ‘Chaotic’ – and they don’t try to shy away from it. Instead, they try to work with the chaos, rather than try to ‘control’ it by moving to one or other of the other domains.
So what I aimed to do in SCAN was be more explicit about this – that it’s the space of ‘Not known’ etc but that it’s okay to be there. All innovation comes from there, for example.
Somewhat as per your previous(ish) comment, we weave the different types of sense-making and decision-making together, a kind of dance across the whole space. The fact that there’s a ‘None-of-the-above’ shouldn’t worry us: it’s what we need at times in order to get our work doen. Yet we also need to be aware of which aspects fit in under which general categories in this sense, because that allows us to tailor our response to suit. That’s part of what I’m aiming for here, anyway.
[A quick note to say that, despite many repeated reminders that his presence here is utterly unacceptable, Snowden has yet again breached that request by posting a comment above. In accordance with the No Asshole Rule, that comment has now been deleted – as will any other future comment from Snowden.
My apologies to Stephen, who replied to Snowden’s comment, and whose comment I’ve also deleted because it had lost its context.
Anyone is welcome to hold any conversation they wish with Snowden, of course. But not here.
Many thanks all.]
@ Tom G
Great article, thanks for pointing it out. As promised, a reflection after reading.
I actually tried your SCAN-drivers on a situation at work where an ambitious employee (turned out pretty ambiguous though) tried to run the office dishwashing machine on washing-up liquid. “Don´t change the rules in the midst action”. Yes, ugly things happened 😉
What I would really like to have, and would like to participate contributing to, are Drivers in the opposite direction. If I have a complex situation, how do I simplify it? It´s easy to say, but hard to implement. I´m involved in an insurance-case where we try to model the Business rules. A simple condition based on received information in a form (application) decides if the information is correct or not. Connect these simple conditions and you soon get a long complicated string forming a rule. Pretty soon people add branching conditions leading to deviating results or loose ends (not-known) and as soon as you show the result to two or more line-managers they all interprets it differently – ambiguous, thanks-a-lot!
When looking at it from that perspective, it´s more of a gravity-thing. Ambiguous/chaos being the black hole sucking everything in, unless you fight it with structure, order and simplification. But then I end up with a framework that looks more like a Dartboard and that only makes sense if you´re striving towards simplification (which I do in this particular case).