Domains and dimensions in SCAN

What are the sensemaking-domains in SCAN? What are the boundaries between those domains?

A great challenge in an earlier comment from Roger Sessions, where he asked me for the mathematical basis for those domains and boundaries. I think he was a bit shocked when I said there wasn’t one 🙂 – but in fact there is such a basis, sort-of, and it’s worth summarising here, out on the surface rather than buried away in the comments.

(Whilst working on this I’ve realised that in some ways this is a repeat of the section ‘The structure of SCAN’ in the post ‘On SCAN, PDCA, OODA and the acronym-soup‘. But it’s probably worth having the extra detail, anyway.)

The dimensions of SCAN

There are three distinct dimensions to SCAN:

• modality – the extent of perceived ‘controllability’ versus ‘possibility and necessity’
• available-time – the amount of time remaining before an action-decision must be made
• repeatability – ability to reliably recreate the same perceived results

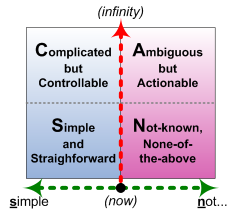
The SCAN frame is usually shown with four apparent domains, derived from the first two dimensions above:

In part, though, this format is mainly for people who are more comfortable with a simple two-axis matrix, or who need to translate across from other domain-oriented frameworks such as Cynefin or the Jungian-based ‘swamp analogy‘. This layout can be somewhat misleading in that the boundaries between apparent domains are not straightforward, and that third dimension of repeatability does also need to be taken into account. We’ll explore how this works in practice in the rest of this article.

Dimension of modality

The ‘horizontal’ dimension for SCAN is a scale of modality of the logic used for sensemaking and decision-making. Modality in this sense is the scope of possibility and necessity; a scale of modality ranges from a simple ‘yes/no’ or ‘true/false’ choice, to an infinity of possibilities. We make a choice from the palette of possibilities on offer in the context, in accordance with what we perceive as the necessity in the context.

In principle, for SCAN, we should draw this as a horizontal graded spectrum of 0..n possibilities for choice, from left (choice of 0..1) to right (choice of 0..infinity). In practice, though, we can put an explicit boundary at the 0..1 point, because the way the choices are usually addressed will change radically on either side of this point. In SCAN, we describe this distinction as a Simple choice, or a Not-simple choice:

Anything that relies on absolute repeatability regardless of agent, on identical circumstances, or on any true/false logic, must by definition be constrained to the Simple side of the scale. This includes almost all machines, most IT, and any rule-bound human context.

The key point is that on the Simple side, there’s only one choice: do it, or don’t do it. Very straightforward. (Whether it actually works, in terms of creating the required results, is another story, of course…) Once the options start to multiply, the choices become more Complicated, but as long as the choice-mechanism is still some form of true/false, it still remains ‘controllable’ – we just need more time to sift through the options and factors and make the ‘right choice’.

But once the options become contextual, or dependent on the skill and capabilities of the agent, or for any reason cannot be absolutely repeatable, that pushes us over the boundary to where a Simple true/false logic is unlikely to work. In other words, it’s Not-simple. And we start to need other ways to work with it – ways that are usually not available from machines or IT, or from inexperienced human trainees. The further over into the Not-simple that it gets, the higher level of skill it will require to get to the equivalent of ‘repeatable’ results – the same perceived outcomes reached via different routes.

One important complication arises from different experiences of ‘simple’ versus ‘complex’. The definition for Simple here is the use of true/false choice-logic, of true/false rules and so on. However, many people experience that as anything but ‘simple’ – especially where rigid rules are applied in contexts that have high natural variability and hence need greater modality. In those contexts, more fluid patterns and guidelines are often experienced as ‘simple’, because it’s easier to use them to achieve the same perceived outcomes.

In those types of circumstances it may be better to change the horizontal scale from a ‘mathematical’ one of modality’, to a more subjective scale of what is experienced as ‘Simple’ versus ‘Not-simple’. We do, however, need to be really clear and explicit as to which type of scale we’re using! 🙂

Dimension of available-time

The ‘vertical’ dimension for SCAN is a straightforward scale of time-available-for-decision. We can use a linear or logarithmic scale scale for this: the choice probably doesn’t matter, although since the time-available can potentially stretch to infinity, a logarithmic scale might make more sense in practice.

The key point here is that as we gain more time before a decision must be made, we also gain the ability to assess a broader range of options. When the time is tightly focussed, we must focus on ‘right here, right now’, the specific point of action, using only what is available at the time. When the time is less tightly focussed, we get to have more choice about how to tackle decisions, about what can be used to enact those decisions, and so on.

It’s a continuous spectrum, of course, so any ‘boundary’ we put along along that vertical axis is going to be somewhat arbitrary. One easy way to partition the timescale is the classic three-way split between Strategy (far-future), Tactics (near-future) and Operations (NOW!). Another – which would obviously be a better fit with the notion of a two-axis matrix – is ‘Time-to-think’ versus ‘No-time-to-think’.

If we use the latter, and combine it with the Simple/Not-simple split on the ‘horizontal-axis’, that gives us a conventional ‘four-domain’ layout for SCAN. So let’s use that for now – always remembering that the position of the vertical-axis boundary between ‘domains’ is an arbitrary choice.

The horizontal-axis here still has that boundary between 0..1 true/false decision-logic to the left, and a true 0..n modal-logic to the right.

So on the left, Time-to-think (‘Complicated’) gives us the rules and categories that we would use in a true/false logic when there’s No-time-to-think (‘Simple’). In other words, it allows its ‘world’ to be more Complicated, but it still expects it to be ‘controllable’, for there to be an identifiable, repeatable ‘right answer’ to every context-related question. In terms of systems-theory, this is the kind of space where we would expect to find ‘hard-systems’ models in use.

And over on the right, Time-to-think (‘Ambiguous’) gives us the patterns and ‘seeds’ – and also the support to work with the uncertainty – for when we work with inherent-uncertainty when there’s No-time-to-think (‘None-of-the-above’). It allows its ‘world’ to be Ambiguous, uncertain, yet also still ‘actionable’, understandable, describable in some sense. In terms of systems-theory, this is the kind of space where we would expect to find ‘soft-systems’ models in use, or concepts of ‘complex-adaptive-systems’ or ’emergent-systems’ and the like.

When it gets down to No-time-to-think in that modal space, though, there often isn’t any way to understand it, or even describe it: it’s too context-specific, too unique to the context, the person or both, often dependent on personal skills and experience that only ‘make sense’ to that individual person. It’s often not sharable as such within anyone else, and there’s no obvious way to make it fit into any predefined category, or even into any identifiable pattern. Hence the label ‘Not-known’, or ‘None-of-the-above’: it simply is. And yet that also is the domain in which perhaps most human work is actually done – and hence should not be ignored…

Dimension of repeatability (variety)

Perhaps the real point about the None-of-the-above domain is that it’s probably the closest we have to ‘the real-world’: everything else is an abstraction.

What we actually have in sensemaking – and, hence, its derived decision-making – is a myth of abstraction: the belief that abstractions are somehow ‘real’. Something ‘makes sense’ because we choose that it should ‘make sense’ in that way: just how much it actually is ‘real’ is often an open question…

In practice, there’s a spectrum of certainty of abstraction, from idea to hypothesis to theory to ‘law’ – lowest-certainty to highest-certainty. The closer we get to ‘law’ (in the scientific sense, at least), the more predictable the context should be – assuming that the ‘law’ is an accurate abstraction, of course. The more predictable it is, the more we can rely on its repeatability – where the same actions deliver the same results. Conversely, the less predictable it is, the less we can rely on the same actions delivering those same results. Which gives us a spectrum of repeatability.

That spectrum of repeatability does sort-of line up with abstraction, but even more so with the variety – in the cybernetics sense – in the actual context. When there’s a mismatch between the type and range of variety that the abstraction can cope with, versus the actual variety in the context – the ‘system’ – then we’re likely to get systemic failure.

This is crucial in enterprise-architecture and the like, because most IT and the like, and most systems that depend on ‘command and control’, are almost by definition constrained to the amount of variety that can be covered by their own true/false logic. The whole point of conventional command-and-control is that it doesn’t permit any variety beyond its own scope. And when the real-world does happen to contain greater variety – which, to be blunt, it often does – then, again, the system will fail. (Though likely that it’d be the real-world, rather than the inadequate abstraction, that would be blamed for the failure…)

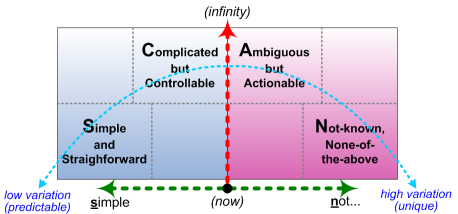
When we put all this together in SCAN, that spectrum of repeatability – or, inversely, of variety – ends up somewhat like this:

When there is low variety in the overall system, it’s relatively Simple to set up straightforward rules, and enact those rules in real-world practice with high to very high probability of repeatable results – including the same results from different agents that use the same rules.

As the variety increases, we need time to be able to identify the various factors and feedback-loops. The system becomes more Complicated, but up to a certain point will still be able to deliver repeatable results with different agents that follow the same more-complicated systemic rules.

As variety continues to increase, there is a crucial cross-over point where doing the same thing can no longer be guaranteed to deliver the same results, sometimes even with the same agent. The crossover into Ambiguous automatically occurs whenever an unaccounted-for factor enters into the supposedly-predictable picture. We can sometimes work out new rules for that new factor, but in some cases there will always be uncertainty, ambiguity – and trying to force the system to fit the lower-variety assumptions of the Complicated ‘domain’ will usually cause systemic failures such as ‘wicked-problems‘ and the like. ‘Soft-systems’ and ’emergent-systems’ methods will help to address the issues here, often developing patterns and guidelines for use at real-time, but as the Complicated ‘domain’, all of these techniques take time – which may not be availability.

As time-available becomes compressed towards real-time, or variety increases still further towards non-repeatable uniqueness, we end up being forced into a ‘domain’ that’s probably best summarised as Not-known or None-of-the-above. Increasingly, the equivalents of ‘repeatable’ results on not repeating the same actions – and it takes increasing levels of skill to guide the context towards desired ‘repeatable’ results. Conversely, repeating the same actions can deliver different results – which again, with skill, may return highly-desirable uniqueness.

Overall, though, note the transitions here: both Simple and Not-known, at the opposite ends of the scale, can work well at or near real-time, whereas Complicated and Ambiguous, in the mid-range, require time to execute. If ‘control’ is required at real-time, it must be Simple: there is no other option. Any other choice either requires more time, or an acceptance that ‘control’ will not work in the context. Again, this point has huge implications for enterprise-architectures.

A possibly-simpler summary

Some quick follow-on points from all of the above:

• In the real world, ‘control’ is a myth – we can simulate some of it, but it often constrains ability to cope with real-world variety such that it’s likely to break down.
• When it does break down at the Operations level, at or near real-time, we’re automatically forced into a None-of-the-above context, which requires skill and experience to bring the context back to a simulation of ‘control’.
• If the skill and experience are not available, or are excluded, the overall system is going to fail – as happens often in misguided attempts at IT-centric ‘business process reengineering’.
• Analysis and experimentation take time to execute – they’re not viable when time-available is compressed down to the real-time level.
• In most real-world systems, time-available will vary: there are periods of intense time-pressure, where only the Simple and the None-of-the-above will work; and there are periods when the time-pressure eases off, which can be used for review and reassessment via a move ‘into’ the Complicated and/or Ambiguous ‘domains’, to prepare for the next high-intensity part of the work-cycle.

I’ll stop there for now, but there’ll be more on this in the upcoming final part of the ‘on sensemaking in enterprise–architecture series‘, and in other future posts.

As usual, comments, anyone?