Knowable and discoverable

“Profound garbage” – that was how he described my work. Well, I can’t complain: at least he described it as ‘profound’… 🙂

Over the past few days there’s been a fair amount that’s gone all kinda philosophical and ‘meta’ on me, and it seems worthwhile to explore a bit about what’s been coming up. Don’t worry, though: it does have real practical applications in the everyday, as you’ll see later.

[An urgent aside: Some of what follows does, in passing, happen to mention the Cynefin framework. It even references back, in passing, to some themes that came and went in some of the earlier versions of Cynefin. But it’s not about Cynefin, at all. This does not critique Cynefin, at all. Please don’t let’s go there again, okay? ‘Nuff said… 🙁 ]

One of the threads in this happened a few days back, when someone – I forget who – posted a piece that contrasted ‘knowable’ with ‘discoverable’. The point there was that ‘knowable’ applies to the more certain side of the things that we come across – things that we can predict, perhaps, or calculate, or derive via some form of formal-logic – whereas ‘discoverable’ was more about the things that we can’t predict, but more just come across in passing. (Like this whole thread, I guess? – recursion again… 🙂 )

What whoever-it-was was saying was that ‘knowable’ could be used as a near-synonym for ‘complicated’, whereas ‘discoverable’ could be used as a near-synonym for ‘complexity’. Yet for me it didn’t quite gel: that kind of ‘discovering’ seemed to me to fit more closely with what’s sometimes referred to as ‘creative-chaos’, the Not-known space where new ideas arise. But there was no real anchor for me to take that idea any further, so – as usual – I just kinda let it sit, and quietly brew away by itself.

Then yesterday, unbeknownst to me, a colleague posted a Tweet that was, yes, arguably critical about Cynefin, and included a pointer to my two-and-some-years-ago post ‘Comparing SCAN and Cynefin‘. One of the responses that came up from that included that comment about ‘profound garbage’ – though the first I heard of any of this was when all of these Tweets starting appearing in my Twitterstream, apparently addressed to me. Ouch…

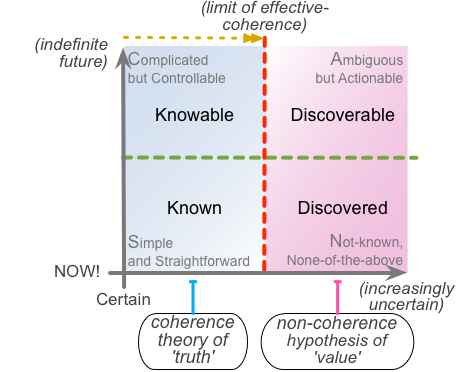
As I said, I’m very careful these days to try to keep out of any discussion on the merits or otherwise of Cynefin: it really isn’t my business, and I prefer to keep it that way. What was much more interesting was the reason why that critic had dismissed my work in that way: it was, he said, because he was “looking for coherence”. At that point I did reply, to ask what he meant by the term ‘coherence’, what he understood it to be. Carefully-polite, to which I received an equally-polite response, in which he pointed to the work of H. H. Joachim, “generally credited with the definitive formulation of the coherence theory of truth“.

Okay, fine, yes, does look interesting: so I chased up the respective Wikipedia entries. But I was, uh, profoundly unimpressed: to me it just seemed to be one of those more-unfortunate examples of circular-reasoning, with ‘truth’ defined as coherency and self-consistency, and coherency in turn defined as ‘truth’. Presumably I was missing something? Either way, I sent a reply saying that I took a rather different view of ‘truth’ and coherency, aligned more with Paul Feyerabend‘s Against Method – in other words, that’s there’s a kind of “anything goes” involved in the story, that ‘truth’ is, in essence, more an artificial construct of its own time and context, and that apparent attributes such as coherency or self-consistency might well prove in practice to be somewhat misleading. And there we left it: no big deal for either of us, no further argument, we each went our separate ways.

Yet this morning, it all kinda came together in one of those classic in-the-shower insights: coherency, as purported-‘truth’, is fundamentally inappropriate for complexity. Coherency is not something that we should expect in true-complexity: or, to frame it the other way round – using Cynefin terminology here – if it’s fully self-consistent, it’s not Complexity, it’s merely Complicated. Perhaps more to the point, trying to assert coherency as a ‘desired-attribute’ for something that incorporates inherent-ambiguities and uncertainties – such as a wicked-problem or a pattern – could well be a very dangerous tactic: trying to apply Complicated-domain methods to such contexts is not a wise move…

Cynefin has some useful things to say about this, but as I said above, I’ll keep out of that: it’s someone else’s model, not mine, after all, so best I don’t go there. What I’ll do instead is link it to SCAN:

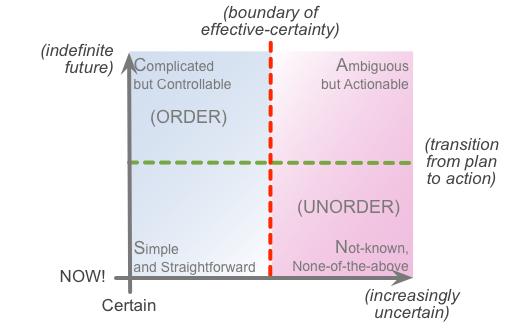
The key to SCAN isn’t the domain-names or any of the other labels: don’t get hung-up on those, they’re literally just labels, nothing more than that. (We could call them all FRED, if you prefer – in homage to Rowland Emmet and his Fantastically Rapid Electronic Device. 🙂 ) Instead, as I described in the post ‘SCAN – some recent notes‘, what matters is those two axes.

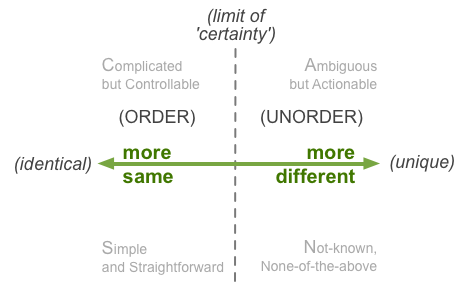
The ‘horizontal’ axis is about, well, a variety of themes such as certainty versus uncertainty, predictability versus unpredictability, sameness versus uniqueness, order versus unorder, or, in this case above, coherence versus non-coherence – they’re all similar enough (and, often related-enough) that you can pick any of them and it’ll come out much the same. Place most-certain or most-predictable or most-same or whatever over on the left-hand side; its opposite extends out to the right, towards infinity:

It’s rare in most real-world situations that we’ll ever get absolute certainty, absolute sameness, absolute predictability. Instead, what we aim for is certain-enough, predictable-enough, and so on, for the requirement at hand. And there’s a real boundary – sometimes sharp-cut, more often somewhat-blurry – between certain-enough and not-certain-enough. That’s what I’ve indicated above as the ‘limit of ‘certainty”, or ‘boundary of effective-certainty’.

The point here is that the tactics and techniques we need to use are often radically-different either side of that boundary: for example, certainty-dependent logic-based methods that aim towards a single ‘solution’ really don’t work with inherently-uncertain and continually-morphing wicked-problems.

Which, if we go back to that initial comment about ‘knowable’ versus ‘discoverable’, does kinda fit here: ‘knowable’ on the left, ‘discoverable’ on the right.

But which… I dunno… still isn’t quite right yet? Not quite enough? So, keep going…

Which brings us to the other axis in SCAN, the ‘vertical’ axis. This is about the amount of time we still have available to us for sensemaking and decision-making before we must take action. We place ‘NOW!’ at (and as) the baseline, with time-available stretching upwards, again potentially to infinity. (For those of us who procrastinate a lot – I wouldn’t be looking at myself here, now would I? 🙁 – the time-before-decision too often really does extend to infinity…)

And once again there’s a very real boundary here – often easily identifiable in humans, if perhaps less so with machines and IT-systems – where, as we get closer towards the ‘NOW!’, the techniques and tactics change: decisions for or about action tend to be distinctly different to decisions within action, at or close to the moment-of-action itself.

We might describe this difference as ‘plan’ versus ‘action’, or ‘theory’ versus ‘practice’ – a point nicely illustrated by the old joke that “In theory there’s no difference between theory and practice; in practice, there is”.

The effective ‘position-in-time’ of that boundary is highly contextual, often dynamic and, again, in some cases also somewhat blurry, but it’s real all right: there is a real difference between what we do in planning, versus what we do to adapt that plan to what’s really happening right-here-right-now.

Yet if that’s so, how do we describe that difference? What came up the other day was a hint from the Cynefin framework, or more specifically out of its past. These days, two of its domains are labelled ‘Simple’ and ‘Complicated’, which I’ve likewise used for the two ‘left-side’ domains in SCAN.

(In part this is intentional, for compatibility-reasons, since in my interpretation of what Cynefin was/is aiming to do, the two frameworks are fairly similar here. To me at least, they diverge a lot over on ‘the other side’: but again, I’m not talking about Cynefin here – just that one fact about the domain-labels.)

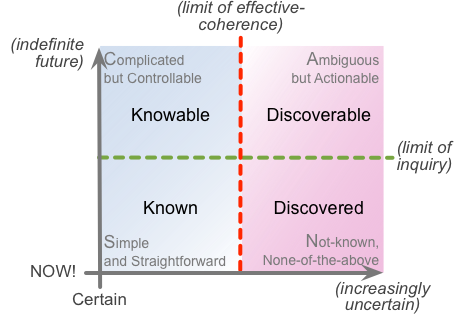
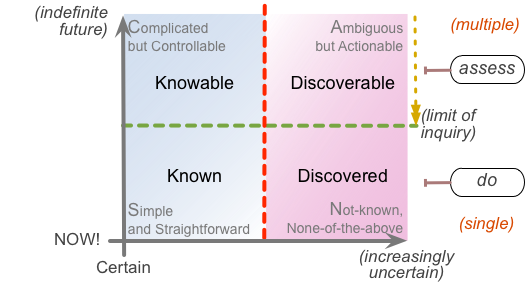
Yet if we go further back in Cynefin’s history, back to the days when it was focused more on knowledge-management concerns rather than complexity in general, those two domains were respectively labelled ‘Known’ (Simple) and ‘Knowable’ (Complicated).

Which, in turn, suggests another way to look at that ‘knowable versus discoverable’ dichotomy mentioned earlier – and that this time does resolve my qualms about it. Because what it suggests is yet another SCAN crossmap:

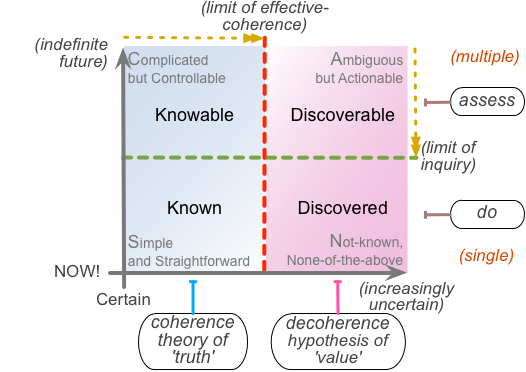
I’ve used the ‘limit of effective coherence’ label on the horizontal-axis boundary, to link to back to the other half of the conversation that started this thread – but I could of course use any other equivalent, such as the original of ‘boundary of effective-certainty’. It really is all ‘much of a muchness’ here.

Anyway, let’s look at this in a bit more detail – horizontal-axis first:

Going back to that initial conversation, about coherence and ‘truth’, in essence it’s about certainty again – things that we can ‘know for certain’. There are things that are somewhat-uncertain, and that we can sort-of link together in a coherent way, even though the terminology or values or whatever kind of differ in some ways from each other. There are lots of real-world examples of that, even in the sciences: our best current theories of cosmology still give a significantly different date than our current best theories of star-formation, for example. But we still can get enough coherence between the various theories to be able to send a space-probe to exact positions in our own solar-system: in other words, ‘good-enough theory’ – or, in effect, the ‘left-side’ of that ‘limit of effective-coherence’.

To get the best results, we might have to do a bit of tweaking, working ‘inside the box’ – the kind of things that analysts do. And whatever results we get here, we can know with reasonable certainty that we’ll get the same results in future if we do the same things in the same way. More or less, anyway.

Over on the other side of that boundary, we can’t know in the same way: instead, we have to kinda discover it. For example, we can’t solve a wicked-problem – reduce it to something ‘known’ – but we can dynamically and repeatedly re-solve it, in accordance with its own strange dance: and the nature of that dance is what we can discover, by careful observation and in-person engagement and the like. The difference between theory and hypothesis, in fact: whilst we might hope that a theory would remain certain, the only thing we can be certain of with an hypothesis is that it’s likely to change!

Moving to the other direction – the vertical-axis:

In this case it’s probably easiest look at this by coming downward, rather than ‘upward’ from the ‘NOW!”-base. Within that ‘knowable and/or discoverable’ space – the analysis / experimentation loop – we can assess multiple options and multiple possibilities. As we get closer towards the ‘NOW!’-point, though, the options get squeezed, until we finally hit a limit for inquiry: we have to take action. Then within the action, the ‘do’-space, we do still have options and possibilities – yet ultimately only one at a time, at the exact moment-of-action.

Overall, this gives us four distinct domains: Known, Knowable, Discoverable, Discovered (or Discovering – active, in contrast to the often somewhat-passive interactions with the purportedly-preordained Known). Note, though, that the boundaries between the domains are, again, often highly dynamic and contextual; and the whole thing is itself often deeply recursive, looping through each of the domains at wildly-varying speeds, as shown in the ‘SCANning the toaster‘ post.

When we do have time to explore, we can explore the limits – theoretical and practical – of the Knowable and the Discoverable. But when we’re tight on time, we’d better stick to what is Known – or face the real and often very-personal challenges of Discovering, and work with what it is that we’ve Discovered in that process.

We can summarise the whole thing visually as follows:

And, using one of the other diagrams from the ‘SCAN – some recent notes’ post, we can summarise the typical types of tactics that come into play dynamically within each of those domains:

That’s about it for now, really.

Practical implications

The main point here is that – as with SCAN in general – this forms a very quick, practical checklist: Known, Knowable, Discoverable, Discovered (or Discovering).

Anything on the Known / Knowable side is going to give us what is effectively ‘doing the same thing leads to the same results’. We might need to tweak it a bit to do that, and iron out a few minor uncertainties, but it’ll get there. What it won’t do – and for the most part isn’t intended to do – is give us anything different, anything new, anything that we don’t already know or that isn’t directly derivable from what we already.

Anything on the Discovered / Discoverable side is going to be, well, always a bit messy and uncertain. Kinda like the World Wide Web, always somewhat in flux, and so well described as “always a little bit broken”. It’s the only place where we’ll find anything new: so if we need something new, something different, we must face what face up to that uncertainty. Another of the key points from that is that once we cross over to the right-side of that boundary, we cannot guarantee results. High-probability does not mean “is going to happen”; low-probability does not mean “won’t happen”; ‘uncertain’ means ‘uncertain’, not “is wrong because it isn’t certain”. Above all, don’t try to ‘control’ it, because attempting to do so will always make things worse.

Anything on the Knowable / Discoverable side of the ‘plan / action’ boundary means that we still have time to do something, to analyse a bit more, experiment a bit more, build a sort-of certainty in the form of rules – for the Known side – or guiding-principles – for the Discover side. The catch is that the longer we stay there, the less we’ll actually get done – because that ‘doing’ only happens when we get right down to the ‘NOW!’, the moment-of-action.

Anything on the Known / Discover side of the ‘plan / action’ boundary allows us to get things done – but only because we’re not still trying to plan. ‘Decision’ literally means ‘to cut away’: and to get things done we have to pare everything right down to the bone, right down to one option, right-here-right-now – one choice which, at the moment-of-action, is actually no choice at all. Which tells us that if we ask people to make choices at the moment-of-action, we’re actually forcing them away from the moment-of-action – which, by definition, slows things down.

So, to put it at its simplest, know where you are at all times within this context-space. Know the ‘rules’ that apply here, the principles that apply here; watch the recursions as the Known, the Knowable, the Discoverable, the Discovering, all loop and weave through each other, often seemingly all in the same moment. And practice at it, and practice at it, until you don’t even notice it at all – yet it’s still always there.

Interesting, I hope? Over to you for comments, anyway.