On metaframeworks in enterprise-architecture

How do we avoid the dreaded ‘framework-wars’ in enterprise-architecture and elsewhere? If there’s no ‘Single Unified Framework For Everything™’, how do we ‘smoosh frameworks together’ to get the best fit for each current context?

The answer: metaframeworks. And, perhaps even more, the disciplines with which metaframeworks are used.

To which you might well ask: what the heck is a metaframework?

Perhaps the best place to start would be a longish quote (you did say you liked being quoted, Chris! 🙂 ) from Chris Lockhart’s brilliant ‘Frankenframeworks‘ post:

Frameworks should be easy to interpret, fast to deploy, amenable to adaptation. They can be picked up and used or tossed aside in favor of something that is a better fit.  The framework shouldn’t fall apart if you decide to remove part of it because it doesn’t suit the problem at hand. The framework can be simple or sophisticated, but either way it should be extensible. Multiple frameworks can be put together or merged to become the methodology for a given situation. These frankenframeworks can be reused. I myself have dozens of them that I reuse or partially reuse on every project I’m on. Keeping this mini-library of frameworks enables me to be agile and flexible.

… The business wants architecture to help it deliver value. Responsiveness, clarity and agility are more important to delivering value than spending a year modeling the world alone in a dark closet someplace.

To that end, a focus on applying the right framework to the right problem is pretty critical. And I don’t think there’s a single “right” answer.

That’s the point: there’s isn’t any “single ‘right’ answer”. Instead, here are a near-infinity of variously-useful answers, variously-valid answers. It’s not about ‘truth’, it’s about usefulness, about value – yet another of those perhaps-subtle-yet-extremely-important distinctions that we come across so often in enterprise-architecture.

Yet how do we identify what is of value, and what is not? How can we know which framework – or, more usually, which bits of which frameworks – to use in which contexts, where, when and how? And, perhaps most important of all, why?

How do we do that, in a way that works? Where do we start? What can we use to guide us in doing this? That’s the kind of question that a framework is supposed to answer: except that what we’ll be working is frameworks themselves. Kind of a lift-yourself-by-your-bootstraps problem, this one…

The way out of this is to re-use a trick from ontology and taxonomy: we make a meta-level. There in ontologies and the like, we define the structure for a type of model via a metamodel, which itself is a specific type of model with some fairly tight constraints on what it can do and describe. A metamodel is just another type of model – a model that’s used to describe models.

Which if you think about it for a moment, means that it looks like we’d need another meta-level – a metametamodel to describe the metamodel to describe models – and then meta upon meta upon meta, all the way to infinity. Fortunately, we don’t have to do that in practice, because we can stop the stack as soon as we get up to a level where the metamodel can describe every aspect of itself: for example, the M3 level in MOF (OMG Meta-Object Facility).

So the same principles apply here: we need a meta-level – a metaframework – that provides guidance on how to create and hack and link between and re-use our frameworks.

Which might suggest that we’d also need metametaframeworks, and so on. Actually, we don’t: every metaframework is just another framework, in exactly the same way that a metamodel is just another type of model. It’s not the framework itself that is ‘meta-‘: it’s how we use the framework that makes it ‘meta-‘.

Which is what we’re actually exploring here: not frameworks as such, but using frameworks with ‘meta-ness’.

[And, we might add, ‘meta-ness’, not ‘meta-mess‘… 🙂 ]

It’s about the overall sensemaking / decision-making process within enterprise-architecture, and how sensemaking-frameworks are used (or, arguably, misused) within that process. So if we paraphrase from Chris’ quote above, the frameworks we need may be simple or sophisticated, but should always be:

• easy to interpret, fast to deploy, amenable to adaptation, extensible
• can be put together or merged with others for the needs of a given situation
• shouldn’t fall apart if some part of it is removed because it doesn’t suit the problem at hand
• may be used, not-used, re-used or adapted according to its fit with the business-need (we fit frameworks to a context, not context to ‘the’ framework)
• supports responsiveness, clarity and agility
• helps architecture to deliver value to the stakeholders, and deliver it fast

We then also need methods to use those frameworks in a ‘meta-‘ manner – and the discipline to use those methods in a way that will work well.

Over the years I’ve written extensively here on metaframeworks and the related disciplines, though not always explicitly with that term. Some of the posts you might find useful on this include:

• Context-space mapping with the Enterprise Canvas – two metaframeworks used together to tackle a business-challenge
• Two Cryptic conversations – the second conversation in this post, with enterprise-architect Sally Bean, covers work that was a direct precursor to SCAN
• On SCAN, PDCA, OODA and the acronym-soup – how sensemaking frameworks are used in the sensemaking / decision-making loop
• Rules, principles and the Inverse-Einstein test – techniques to identify and work with inherent-uncertainty
• Between the boxes – the disciplines on how to link and move between the ‘boxes’ of a framework
• Sensemaking and the swamp-metaphor, and Sensemaking – modes and disciplines – another metaframework, with description of how to use it in practice
• Decision-making – belief, fact, theory and practice – the same metaframework-principles applied to decision-making in conjunction with sensemaking
• What I do and how I do it – metaframeworks applied at the scale of entire industries or disciplines

Also my book Everyday Enterprise Architecture is largely about the application of metaframeworks in everyday real-world enterprise-architecture challenges – though again I don’t use the term ‘metaframeworks’ there, not least because it tends to frighten people off! 🙂

A key theme for metaframeworks is switching between and comparing multiple views, a process and discipline quite a few folks refer to as ‘lenscraft‘. For example, see these two presentations:

• by Richard Veryard: The Land of Lenscraft
• by Nigel Green: Lost in Translation? – multiple lenses in business-analysis

Each ‘lens’ is a way of seeing; in the same way, each ‘box’ in a conventional framework is an intentional category, a ‘lens’, a ‘way of seeing’.

The only significant danger here is if people think that the ‘boxes’ are all that the framework is: “a simplistic categorisation tool”, to quote an unnamed Tweeter referenced in my ‘Between the boxes‘ post. So as in that post, and in the technique that I describe as ‘context-space mapping’, we need to emphasise not just the ‘boxes’ – the categories or lenses – but also:

• relations between the boxes
• the dynamics of and for moving ‘between the boxes’
• the guiding context, concept and constraints for the overall frame

We also use whole frameworks as ‘lenses’, switching between them, comparing them, and also overlaying them on top of each other, to deliver new insights. (This is described in some detail in the book Everyday Enterprise-Architecture, and in this series of posts on ‘meta-methodology‘, from before the development of context-space mapping as a distinct method.) Overlay-frameworks are like multiple lenses overlaid on top of each other, or perhaps different rotations of a kaleidoscope: different things are emphasised or de-emphasised, different patterns come into and out of view.

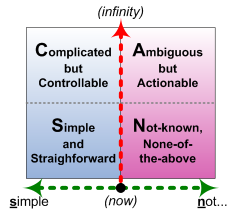
Let’s use the SCAN framework as an example here:

We can use this as a sensemaking framework in its own right, particularly in conjunction with its counterpart on decision-making. We’d use it to guide a kind of conceptual dance, moving back and forth between the different ‘lenses’ to see what they show us, and trying on the overall context, and different parts of the context – hence ‘context-space mapping’ – to see where and how and why and in what ways they might or might not ‘make sense’.

And we can also use SCAN and suchlike as metaframeworks, to guide thinking about other frameworks, and the hacks and adaptations and ‘smooshing-together’ that are needed in order to create useful context-specific frameworks. A simple example of this would be where we could use SCAN to explore the nature of the supposed boundaries between its own domains:

• Simple: the boundaries between the domains are fixed, explicit, and absolute (either/or)
• Complicated: the boundaries between the domains are explicit and absolute, but can move somewhat along each axis (as in the way that IT can make analytic decision-making faster, and hence ‘closer’ to real-time)
• Ambiguous (‘Complex’): the boundaries between the domains may blur (such as where one or both of the axes are a ‘both/and’ spectrum rather than a strict either/or distinction)
• Not-known (‘Chaotic’): there are boundaries, and there are no boundaries, all in the same moment

Hence, as described in ‘Domains and dimensions in SCAN‘, the SCAN frame can be viewed as a Simple-type 2×2 matrix, but it is also a lot more than that. The red-line boundary on the horizontal-axis has a real and definite edge to it – the Inverse-Einstein test – yet it’s also a point on a continuous spectrum of modality from fully-repeatable to never-repeatable; and the view into a context will frequently transition between either side of that boundary. Likewise, the dotted-line boundary on the horizontal axis – the transition between ‘considered’ versus real-time sensemaking and decision-making – is always somewhat blurred, and only indicates an exact transition at the point just before the moment of action.

In effect, there are layers of meaning implied within those seemingly-certain boundaries, depending on how we view them. Given that insight, we can apply the same kind of review to apparent boundaries in other frameworks, to give us more clarity about what those respective domain-boundaries actually mean in sensemaking / decision-making practice.

To do this in more depth, we would use SCAN or whatever in conjunction with disciplines from systems-thinking and the like, to provide a kind of guided continuous-loop action-learning process. In an earlier post I outlined seven systems-thinking principles that work well for this:

• rotation – switching between views or ‘boxes’ in a framework or list
• reciprocation – balance across a system
• resonance – feedback-loops in a system
• recursion – self-similar patterns at every scale
• reflexion – the whole contained within the part
• mismatch – cognitive-dissonance to break ‘out of the box’
• serendipity – allow ideas to emerge ‘at random’

That list of principles itself provides a simple type of rotation, as does the visual pattern of the SCAN ‘domains’. (A ‘rotation’ isn’t necessarily linear, by the way – a simple rotation does, of course, but there’s always a lot more available than just the Simple option. 🙂 ) Each of those items is very simple in itself, and it doesn’t take long to memorise what they each mean in practice, and how to scan quickly through their implications in each domain or aspect of a context.

More often, though, we would use the principles in combination with each other, and in conjunction with mapping of relations, dynamics, context, context, constraints and overlays. For example:

— the assessment of boundaries in SCAN as above combines rotation with recursion.

— a checklist combines rotation and mismatch – in an action-checklist, we’re looking for what isn’t there (rather than a follow-the-step-by-step process, which assumes that everything is there).

— the desire to add columns or sections to a framework often arises from another version of rotation plus mismatch – in this case, finding a ‘mismatch’ from what’s not in the frame.

— applying rotation, reciprocation, resonance and recursion to Business Model Canvas highlighted its implicit asymmetry (mismatch) between supplier-side and customer-side, which became a key design-theme for the Enterprise Canvas model-type.

— applying comparison, overlay, rotation and mismatch indicated the changes that would be needed to adapt Business Model Canvas for not-for-profit and government contexts.

— using software-patterns, architecture-patterns and the like is a form of reflexion – applying a small abstract ‘part’ to a larger concrete ‘whole’ – though we also need rotation, reciprocation, resonance, probably recursion, and certainly mismatch to identify how to adapt the pattern to the specific context in play.

— using deliberately ‘wrong’ or ‘absurd’ mismatch is often a key tactic to elicit serendipity in innovation and idea-development.

— see the post ‘Sensemaking – modes and disciplines‘ for an example of ‘lenscraft’ that uses rotation, relations and dynamics to switch between ‘lenses’, and mismatch to highlight when and how and where to switch between ‘lenses’, in a way that’s designed to trigger serendipity to guide understanding of a context.

— see the post ‘What I do and how I do it‘ for a systematic process of applying comparison, reciprocation, recursion, reflexion and mismatch to re-think and re-structure whole disciplines or entire industries.

Enough for now, anyway. In the next post in this series we’ll explore how all of this hacking and ‘smooshing-together’ works in real-world practice, with some detailed worked-examples from my own enterprise-architecture developments.

Over to you, perhaps?